期望货币
供需平衡
最短路径
盈亏平衡点
某厂生产的某种电视机,销售价为每台2500元,去年的总销售量为25000台,固定成本总额为250万元,可变成本总额为4000万元,税率为16%,则该产品年销售量的盈亏平衡点为(9)台(只有在年销售量超过它时才能盈利)。
- 盈亏平衡点(Break Even Point, BEP)通常是指全部销售收入等于全部成本时(销售收入线与总成本线的交点)的产量。
- 单件产品税后收入=2500×(1-16%)=2100元
- 单件产品边际成本=可变成本总额/总销量=4000万元/25000=1600元
- 单件产品边际利润=单件产品税后收入-单件产品边际成本=2100-1600=500元
- 盈亏平衡点产量=固定成本/单件产品边际利润=250万/500=5000台。
某通信线路工程的工程费为500万元,其中建筑安装工程费为350万元;建设单位管理费费率为1.8%;工程质量监督费费率为0.15%,则建设单位管理费为(1)和工程质量监督费为(2)
- 建设单位管理费为500×1.8%=9万。
- 工程质量监督费是指工程质量监督机构对通信工程造价进行质量监督所发生的费用。计费标准和计算规则为:通信线路、管道等工程按建筑安装工程费的0.15%计取;通信设备安装工程按建筑安装工程费的0.25%计取。此项费用在建设单位管理费中列支。
- 本题,工程质量监督费为350×0.15%≈0.53万。
运筹学
甲、乙、丙、丁4人加工A、B 、C、D四种工件所需工时如 下表所示。指派每人加工一种工件,四人加工四种工件其 总工时最短的最优方案中,工件B应由( 丁 )加工。
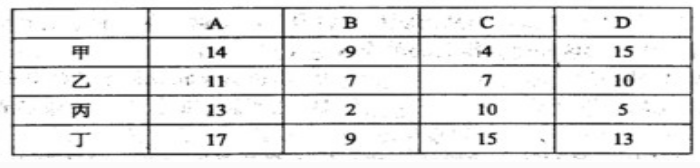
本题考查数学(运筹学)应用的能力。
本题属于指派问题:要求在4×4矩阵中找出四个元素,分别位于不同行、不同列,使其和达到最小值。
显然,任一行(或列)各元素都减(或加)一常数后,并不会影响最优解的位置,只是目标值(指派方案的各项总和)也减(或加)了这一常数。
我们可以利用这一性质使矩阵更多的元素变成0,其他元素保持正,以利于求解。

累积减数11+2+4+5+6=28。
对该矩阵,并不存在全0指派。位于(1,3)、(2,1)、(3,4)、(4,2)的元素之和为1,是最小的。因此,分配甲、乙、丙、丁分别加工C, A, D,B能到达到最少的总工时28+1=29。
最大收益
- (最大收益问题)某公司现有400 万元用于投资甲、乙、丙三个项目,投资额以百万元为单位,已知甲、乙、丙三项投资的可能方案及相应获得的收益如下表所示:
则该公司能够获得的最大收益值是( )百万元。
A、17 B、18 C、20 D、21
依题意,对4百万元资金可以集中投资于某个项目,也可以拆分投资于某两个或3个项目。例如,若4 百万元资金集中投资于项目曱,则可以获得的收益值是10百万元;若对项目曱投资1百万元,对项目乙投资 2百万元,对项目丙投资1百万元,则可以获得的收益值是18百万元(即4+9+5=18 )。
生产某种商品有两个建厂方案:(1)建大厂,需要初期投资500万元。如果产品销路好,每年可以获利200万元;如果销路不好,每年会亏损20万元。(2)建小厂,需要初期投资200万元。如果产品销路好,每年可以获利100万元;如果销路不好,每年只能获利20万元。
市扬调研表明,未来2年这种产品销路好的概率为70%。如果这2年销路好,则后续5年销路好的概率上升为80%;如果这2年销路不好,则后续5年销路好的概率仅为10%。为取得7年最大总收益,决策者应( )。
A.建大厂,总收益超500万元
B.建大厂,总收益略多于300万元
C.建小厂,总收益超500万元
D.建小厂,总收益略多于300万元
