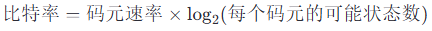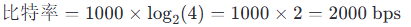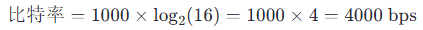差错控制编码是一种用于检测和纠正数据传输过程中可能发生的错误的技术。它通过在原始数据中添加额外的冗余信息来实现这一点。差错控制编码可以分为两大类：检错编码和纠错编码。以下是几种常见的差错控制编码技术：
检错编码
- 奇偶校验码（Parity Check）
- 原理：通过在数据位后面附加一个额外的位（奇偶位），使得数据位中1的总数为奇数或偶数。
- 特点：只能检测单个位错误，不能纠正错误。
- 应用：简单且成本低廉，用于许多存储系统和通信系统中。
- 循环冗余校验码（CRC, Cyclic Redundancy Check）
- 原理：通过使用多项式除法生成一个冗余码，附加在数据后面。
- 特点：可以检测多种类型的错误，包括多位错误。
- 应用：广泛应用于通信系统、存储系统和网络协议中。
纠错编码
- 海明码（Hamming Code）
- 原理：通过在数据位中插入额外的校验位，使得每个校验位能够检测一定数量的数据位。
- 特点：不仅可以检测错误，还能纠正单个位的错误。
- 应用：用于存储系统、通信系统和网络协议中。
- Reed-Solomon 码（RS 码）
- 原理：基于有限域上的多项式运算，可以在数据中添加冗余信息。
- 特点：可以检测和纠正多位错误。
- 应用：广泛应用于数据存储、无线通信、卫星通信等领域。
- BCH 码（Bose-Chaudhuri-Hocquenghem 码）
- 原理：一种特殊的线性分组码，基于有限域上的多项式运算。
- 特点：可以检测和纠正多位错误。
- 应用：用于数据存储和通信系统中。
- Turbo 码（Turbo Codes）
- 原理：使用迭代解码算法，可以检测和纠正多位错误。
- 特点：接近香农极限，提供非常高的编码增益。
- 应用：广泛应用于无线通信系统，如3G、4G LTE和5G网络。
- 低密度奇偶校验码（LDPC, Low-Density Parity-Check Codes）
- 原理：基于稀疏矩阵的编码方案，使用迭代解码算法。
- 特点：接近香农极限，具有良好的性能。
- 应用：广泛应用于无线通信、光通信和数据存储系统。
差错控制编码的应用
- 通信系统：用于无线通信、卫星通信等。
- 数据存储：用于硬盘驱动器、固态硬盘等。
- 网络协议：用于TCP/IP协议栈中的CRC校验。
- 数字媒体：用于音频和视频编码，如CD、DVD、蓝光等。
总结
- 检错编码：用于检测错误，但不能纠正错误。
- 纠错编码：不仅可以检测错误，还能纠正错误。
- 应用：广泛应用于通信、存储、网络等多个领域。
差错控制编码对于确保数据的可靠传输至关重要，特别是在易受干扰的环境中。根据不同的应用场景和需求，可以选择合适的差错控制编码技术。
海明校验码（Hamming Code）是一种能够检测并纠正单个比特错误的线性分组码。它通过在原始数据位之间插入监督位（也称为校验位或冗余位）来实现这一功能。下面我将解释如何构建一个海明校验码，并给出一个具体的例子。
码距就是两个码字C1与C2之间不同的比特数。在数据中间加入几个校验码，码距均匀拉大，将数据的每个二进制位分配在几个奇偶校验组里，当某一位出错，会引起几个校验位的值发生变化。海明不等式:校验码个数为K，2的K次方个校验信息，1个校验信息用来指出”没有错误”，其余2k-1个指出错误发生在那一位，但也可能是校验位错误，所以满足m+k+1<=2k。
海明校验码的构建步骤
海明码默认使用偶校验。
奇偶校验
奇校验：一串由0和1组成的序列中1的个数如果为偶数则在前面加个1，使1的个数变成奇数，否则加0。
偶校验：一串由0和1组成的序列中1的个数如果为奇数则在前面加个1，使1的个数变成偶数，否则加0。
例：
1111 奇校验就是 11111 偶校验就是 01111
1110 奇校验就是 01110 偶校验就是 11110
确定监督位的数量：
放置监督位：
计算监督位的值：
每个监督位负责检查一组数据位，这些位由该监督位的索引决定。比如第 1 位监督位负责检查所有奇数位；第 2 位监督位负责检查第 2 位、第 3 位、第 6 位、第 7 位等。
监督位的值由其负责的数据位的奇偶性决定。如果负责的数据位中 1 的个数为奇数，则监督位为 1；如果为偶数，则监督位为 0。
发送数据：
发送包含监督位和数据位的新编码。
接收和校验：
接收端使用相同的规则计算每个监督位的值，并与接收到的监督位值进行比较。
如果所有监督位都匹配，则认为没有错误。如果有不匹配的情况，可以通过监督位的组合来定位错误位的位置，并纠正错误。
示例数据
（1）可知m=9，m+k+1<=2的k次方，可知k最小值为4，所以总共要传输的数据位数为9+4=13；
（2）海明校验码放在索引号为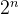
的位（n=0,1,2,…,k-1）上，本例中k=4，所以校验位的索引为第1，2，4，8位，于是在下表中把这几位空出来
| 索引号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| H1 | H2 | 1 | H4 | 0 | 1 | 1 | H8 | 0 | 1 | 1 | 0 | 0 |
（3）列出进制转换表：
| 索引号 | 8（ ） | 4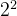（ ） | 2（ ） | 1（ ） |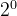
| 3 | 0 | 0 | 1 | 1 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 |
上表中，先说每一行的内容：从第二行开始，每一行的第一列代表索引号，这个索引号是除去了海明校验位之外的其他所有位。后面几列为该索引号对应的二进制表示，其位数取决于第（1）步计算得出的海明校验码的位数，比如第二行，索引号是3，十进制3对应的二进制就是0011，之所以用4位表示是因为这段信息码需要4个海明校验位。
再看列信息：第一行最右边数字1所对应的列里，出现1的，就表示可以用第H1位完成校验，出现数字0则表示不能用H1位进行校验，因此，由上表可知：
校验位H1负责校验：第3，5，7，9，11，13位（上表黄色高亮显示部分），对应位置上的值进行异或得：1⊕0⊕1⊕0⊕1⊕0=1，由于海明校验做的是偶校验，则H1=1；
校验位H2负责校验：第3，6，7，10，11位（上表蓝色高亮显示部分），对应位置上的值进行异或得：1⊕1⊕1⊕1⊕1=1；
校验位H4负责校验：第5，6，7，12，13位，对应位置上的值进行异或得：0⊕1⊕1⊕0⊕0=0；
校验位H8负责校验：第9，10，11，12，13位，对应位置上的值进行异或得：0⊕1⊕1⊕0⊕0=0。
（4）得到最终要传输的数据串为
| 索引号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
接收端：
（1）进行校验：
若此时接收方收到的数据相比源数据，在第11位发生了错误：
| 索引号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
接收方先按照第③步中类似的方式进行计算校验，区别在于要加上校验位自身这一位，即：
C1的值为第H1，3，5，7，9，11，13位上的值进行异或，计算结果为1（1⊕1⊕0⊕1⊕0⊕0⊕0=1)应该为0（因为默认使用偶校验1的位数为偶数） 所以有一位错误，也就是C4的结果正确。
C2的值为第H2，3，6，7，10，11位上的值进行异或，计算结果为1
C4的值为第H4，5，6，7，12，13位上的值进行异或，计算结果为0
C8的值为第H8，9，10，11，12，13位上的值进行异或，计算结果为1
（2）错误位判定：
由于海明校验采取的是偶校验，所以判断出C4监督式包含的数据位无错，错误位发生在C1,C2,C8三个监督式包含的位上。
此时的做法是：①找到C1,C2,C8这三个监督式共同包含的位；②找出共同包含的位之后，再剔除掉在C4中出现过的位（因为已经验证过C4监督式中的位是正确的）；③剩下的位就是发生传输错误的位。
这三个监督式都包含第11位，同时C4监督式中没有第11位，因此出错的位就是第11位。
这样我们就完成了海明校验码的一个基本示例。请注意，海明校验码只能纠正单个比特的错误，如果同时有两个或更多的比特位出错，则无法正确地纠正。
CRC校验码
CRC（Cyclic Redundancy Check）校验的步骤可以通过一个简单的例子来说明。这里我们将使用一个常见的生成多项式 G(x) = x^3 + x^2 + 1 或者二进制表示为 1101，这将产生一个3位的CRC校验码。
假设我们要发送的数据为 11010011101100，我们来一步步地演示如何生成CRC校验码，以及如何在接收端验证数据的正确性。
发送端
- 初始化:
- 数据多项式
M(x) 表示为 11010011101100。
- 生成多项式
G(x) 为 1101。
- 添加尾部零:
- 因为CRC校验码的长度是生成多项式的位数减1，这里是3位，所以我们在数据后面添加3个零：
11010011101100000。
- 计算CRC校验码:
- 使用模2除法（异或运算）计算多项式
M'(x) = 11010011101100000 除以 G(x) = 1101 的余数。
- 首先，由于
M'(x) 的最高次幂为14，而 G(x) 的最高次幂为3，所以我们从 M'(x) 的最高次幂开始，直到比 G(x) 的最高次幂低的位置。
- 对于每一步，我们找到与
G(x) 最高位对齐的位置，然后进行异或运算。
- 异或运算:
- 开始时，
M'(x) 的前四位是 1101，与 G(x) 相同，所以异或的结果为 0000，移除这部分，留下 0000011101100000。
- 接下来，前四位是
0000，不需要进行异或，直接将 0000011101100000 向右移动一位，变成 000001110110000。
- 重复这个过程，直到
M'(x) 的前四位与 G(x) 对齐，进行异或，然后继续向右移动。
- 继续这个过程，直到
M'(x) 的剩余部分比 G(x) 短。
- 最终余数为
R(x)。
- 添加CRC校验码:
- 将最终余数
R(x) 附加到原始数据的末尾，形成发送数据。
练习（两百）
- 若信息码字为 11100011，生成多项式 G(x)=x5+x4+x+1 ，则计算出的 CRC 校验码为（）。
A. 01101
B. 11010
C. 001101
D. 0011010
----------------------------------------
答案：
B
解析：
这里要做类似的除法操作
11100011 为被除数
G(x)=x5+x4+x+1 ，生成 110011 ，为除数
CRC 校验码的规则下，被除数后面要添 (n-1) 个 0，n 是被除数的位数，也就是 1110001100000。
这里的除法做的是异或操作，也就是
00 -> 0
11 -> 0
10 -> 1
01 -> 1
【0 ⊕ 0 = 0，1 ⊕ 0 = 1，0 ⊕ 1 = 1，1 ⊕ 1 = 0（同为 0，异为 1）】
若信息码字为11100011，生成多项式 G（X）=X5+X4+X+1，则计算出的 CRC 校验码为 （16） 。
（16）A．01101 B．11010 C．001101 D．0011010
答案 ： B
