网工 加密技术、数字签名、数字信封

对称加密的过程

  1. 密钥生成：
    • 在对称加密中，首先需要生成一个密钥。这个密钥将用于加密和解密数据。
    • 密钥应该足够强大，以抵御暴力破解攻击。现代对称加密算法通常使用128位、192位或256位长度的密钥。
  2. 加密过程：
    • 明文：需要加密的原始数据。
    • 加密算法：选择一个对称加密算法，如AES（Advanced Encryption Standard）、DES（Data Encryption Standard）或3DES（Triple DES）等。
    • 加密：使用选定的加密算法和密钥对明文进行加密，生成密文。
  3. 解密过程：
    • 密文：加密后的数据。
    • 解密算法：使用相同的加密算法进行解密。
    • 解密：使用相同的密钥对密文进行解密，恢复成原始的明文

示例

假设我们使用AES加密算法进行对称加密。

  1. 生成密钥：
    • 生成一个256位的AES密钥。
  2. 加密过程：
    • 明文：Hello, World!
    • 加密算法：AES-256
    • 加密：使用AES-256算法和密钥对明文进行加密，得到密文。
  3. 解密过程：
    • 密文：通过加密步骤得到的密文
    • 解密算法：AES-256
    • 解密：使用相同的AES-256算法和密钥对密文进行解密，得到原始的明文Hello, World!。

对称加密算法

常见的对称加密算法包括：

  1. AES（Advanced Encryption Standard）：目前最广泛使用的对称加密标准之一，支持128位、192位和256位密钥长度。
  2. DES（Data Encryption Standard）：早期的对称加密标准，现在被认为不够安全，已被AES取代。使用56位加密
  3. 3DES（Triple DES）：通过三次应用DES算法来增强安全性。112位密钥、三个密钥k1/K2/K3 K1=K3(56*2) K2用于解密。
  4. 3DES中的K1=K3，加密过程是使用K1对M进行DES加密得到C1，然后使用K2对C1进行DES解密得到C2，最后使用K1对C2进行DES加密得到C3。
  5. IDEA （128位密钥）
  6. Blowfish：一种较早的对称加密算法，支持可变长度的密钥。
  7. Twofish：一种设计用于替代DES的对称加密算法，支持128位、192位和256位密钥长度。
  8. RC-5、RC-4

对称加密的应用场景

对称加密通常用于以下场景：

  • 数据加密：加密文件、数据库、备份等。
  • 网络通信：加密传输的数据，如SSL/TLS中的数据加密部分。
  • 即时通讯：加密聊天消息。
  • 硬件加密：加密硬件设备，如USB闪存盘、硬盘等。

对称加密有2种：置换和代换 ABC 代换为CBA ABC 转换XYZ

对称加密有常规加密算法和共享加密算法

公钥加密算法（常用于数字签名）

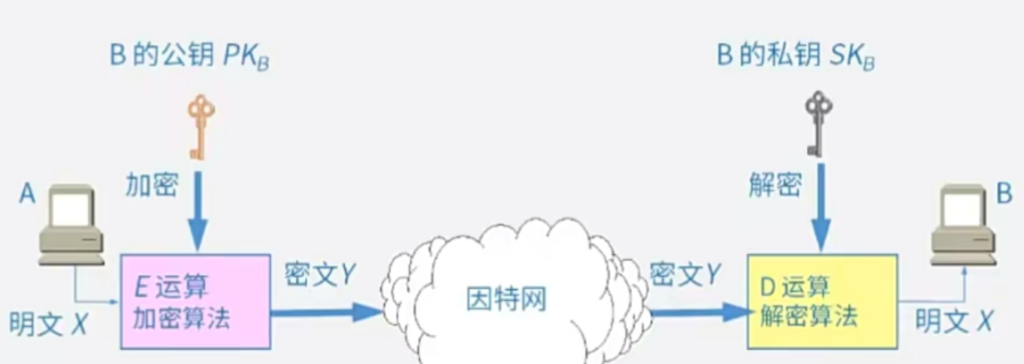
由B产生一对密钥，

RSA 算法举例

以下是一个简单的 RSA 加密算法的举例：

首先，选择两个大质数 p 和 q ，假设 p = 5 ， q = 11 。

计算 n = p * q = 5 * 11 = 55 。

计算欧拉函数 φ(n) = (p - 1) * (q - 1) = 4 * 10 = 40 。

选择一个整数 e ，使得 1 < e < φ(n) ，并且 e 与 φ(n) 互质。假设 e = 7 。

计算 d ，使得 (e * d) % φ(n) = 1 。通过计算可得 d = 23 。

此时，公钥为 (n, e) ，即 (55, 7) ，私钥为 (n, d) ，即 (55, 23) 。

假设要加密的明文 m = 9 。

加密过程： c = m^e % n = 9^7 % 55 = 47 ，得到密文 c = 47 。

解密过程： m = c^d % n = 47^23 % 55 = 9 ，成功解密得到明文 m = 9 。

需要注意的是，在实际应用中，p 和 q 会选择非常大的质数，以保证加密的安全性。

DH算法（密钥交换算法）

DH 公钥加密算法

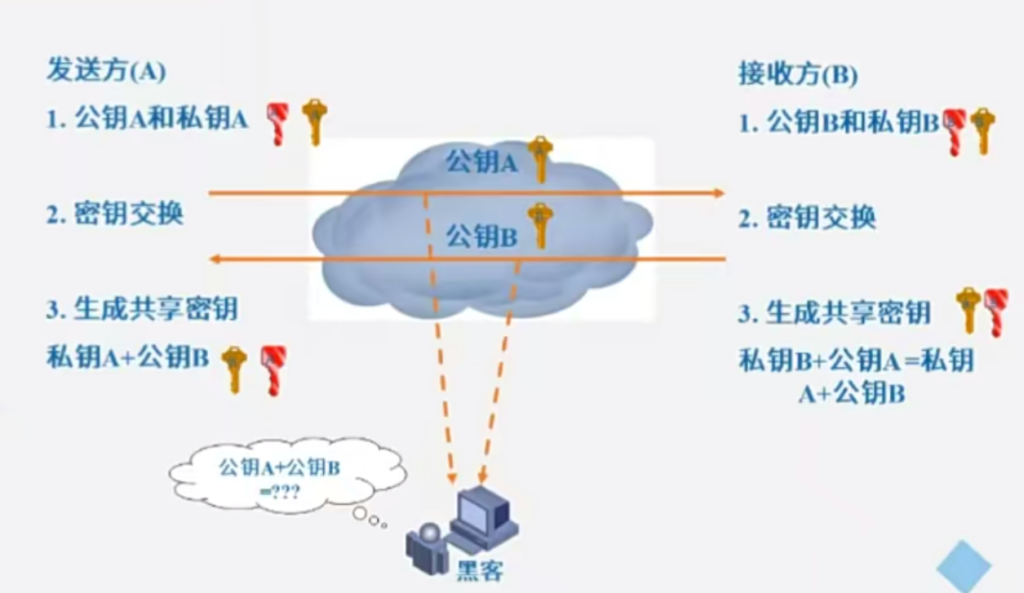
以下是一个简单的 Diffie-Hellman（DH）算法的举例：

假设 Alice 和 Bob 想要通过 DH 算法协商一个共享密钥。

首先，选取一个大的素数 p 和一个本原根 g 。假设 p = 23 ， g = 5 。

Alice 选择一个秘密整数 a = 6 ，然后计算 A = g^a mod p = 5^6 mod 23 = 8 ，并将 A = 8 发送给 Bob。

Bob 选择一个秘密整数 b = 15 ，计算 B = g^b mod p = 5^15 mod 23 = 19 ，并将 B = 19 发送给 Alice。

Alice 收到 B 后，计算共享密钥 K = B^a mod p = 19^6 mod 23 = 2 。

Bob 收到 A 后，计算共享密钥 K = A^b mod p = 8^15 mod 23 = 2 。

这样，Alice 和 Bob 就成功地协商出了相同的共享密钥 K = 2 ，而在这个过程中，他们的秘密整数 a 和 b 并没有在网络中传输，攻击者即使获取了 A 、 B 、 p 和 g ，也很难通过计算得出 a 和 b ，从而保证了密钥协商的安全性。

需要注意的是，在实际应用中，p 通常是一个非常大的数，以确保安全性。

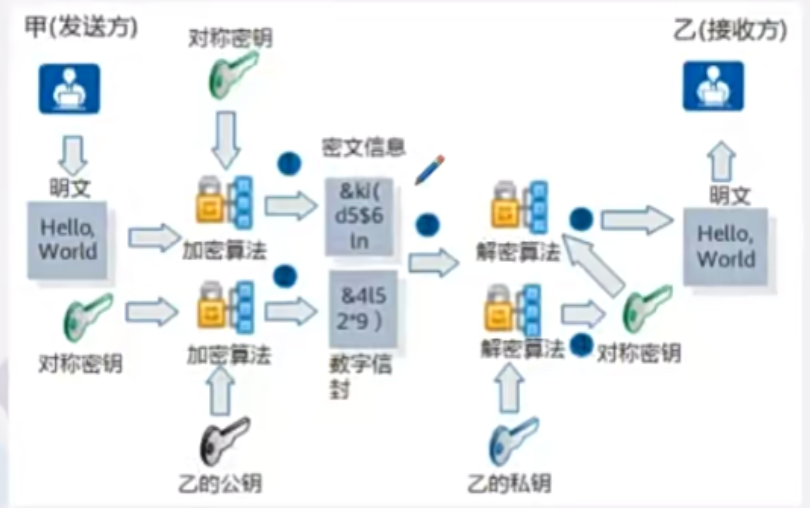
数字信封

甲事先获得乙的公钥，具体加解密过程如下：

  1. 甲使用对称密钥对明文进行加密，生成密文信息。
  2. 甲使用乙的公钥加密对称密钥，生成数字信封。
  3. 甲将数字信封和密文信息一起发送给乙。
  4. 乙接收到甲的加密信息后，使用自己的私钥打开数字信封，得到对称密钥。
  5. 乙使用对称密钥对密文信息进行解密，得到最初的明文。

数字签名

数字签名不保证信息的机密性，基于非对称加密算法，用于核实发送方的身份。这里的密文不是加密的。

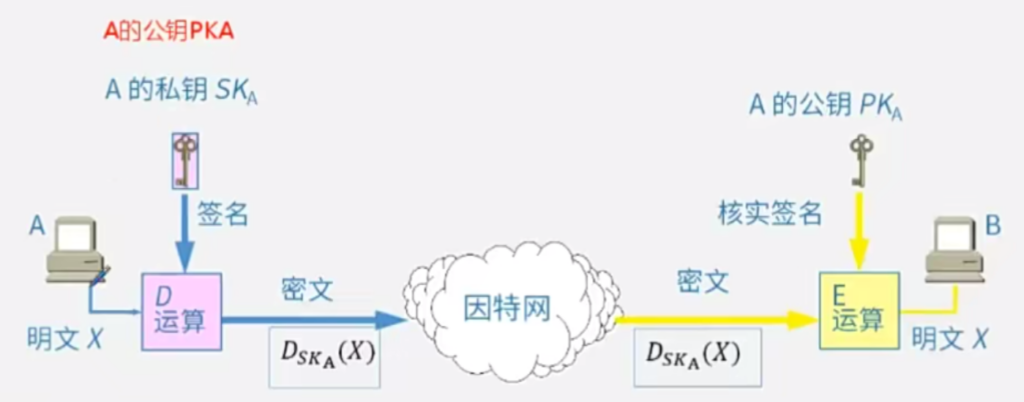
数字签名是一种用于验证数字文档的真实性和完整性的加密技术。它使用非对称加密算法来确保数据的来源可靠并且未被篡改。

数字签名与数字信封的区别

数字信封和数字签名都是在信息安全领域内广泛使用的加密技术，但它们的目的和使用场景有所不同。下面是这两种技术的主要区别：

数字信封 (Digital Envelope)

  • 目的：保护数据的机密性，即确保数据在传输过程中不被第三方窃听或读取。
  • 工作原理：
    • 发送方使用一个对称加密算法（如AES）对消息进行加密。
    • 发送方再使用接收方的公钥加密这个对称密钥，形成“数字信封”。
    • 接收方使用自己的私钥解密数字信封，获取对称密钥。
    • 接收方使用对称密钥解密消息。
  • 优点：对称加密算法通常比非对称加密算法更快，因此可以有效地保护大量数据的机密性。
  • 缺点：不提供发送者身份验证或防止数据篡改的功能。

数字签名 (Digital Signature)

  • 目的：验证数据的完整性和发送者的身份，确保数据没有被篡改并且确实来自声明的发送者。
  • 工作原理：
    • 发送方使用哈希函数计算消息的摘要。
    • 发送方使用自己的私钥对摘要进行加密，生成数字签名。
    • 发送方将消息和数字签名一同发送给接收方。
    • 接收方使用发送方的公钥解密数字签名，得到原始摘要。
    • 接收方独立地计算接收到的消息的摘要，并与从数字签名中解密出的摘要进行比较。
  • 优点：提供了数据完整性和发送者身份认证。
  • 缺点：通常较慢，不适合直接用于加密大量数据。

主要区别总结

  1. 用途：
    • 数字信封：主要用于保护数据的机密性。
    • 数字签名：主要用于验证数据的完整性和发送者的身份。
  2. 加密密钥：
    • 数字信封：使用公钥加密对称密钥，对称密钥用于加密数据。
    • 数字签名：使用私钥加密消息摘要。
  3. 解密密钥：
    • 数字信封：接收方使用私钥解密数字信封获得对称密钥，然后使用对称密钥解密数据。
    • 数字签名：接收方使用发送方的公钥解密数字签名以验证其真实性。
  4. 安全性：
    • 数字信封：保证数据在传输过程中的保密性。
    • 数字签名：保证数据的真实性和完整性。
  5. 效率：
    • 数字信封：通过结合使用对称加密和非对称加密提高效率。
    • 数字签名：仅使用非对称加密，处理速度较慢。

在实际应用中，为了同时提供数据的机密性和完整性验证，通常会将数字信封和数字签名结合起来使用。例如，发送方先使用对称密钥加密消息，然后对这个密钥进行数字签名，最后将加密过的密钥和消息一起封装进数字信封中。接收方则先验证数字签名，确认密钥的有效性后，再使用该密钥解密消息。这样既确保了消息的机密性也验证了其完整性和来源的真实性。

哈希算法

哈希算法=报文摘要算法=HASH算法=散列算法=数字指纹

3DES 加密过程

3DES中的K1=K3，加密过程是使用K1对M进行DES加密得到C1，然后使用K2对C1进行DES解密得到C2，最后使用K1对C2进行DES加密得到C3。

ECC（Elliptic Curve Cryptography，椭圆曲线密码学）是一种基于椭圆曲线数学理论的公钥加密技术。与传统的RSA等公钥加密算法相比，ECC在相同安全强度下所需的密钥长度更短，计算效率更高，因此在资源受限的环境中（如移动设备和物联网设备）特别受欢迎。

Table of Contents

→ Index